First-hitting-time model

In statistics, first-hitting-time models are a sub-class of survival models. The first hitting time, also called first passage time, of a set $A$ with respect to an instance of a stochastic process is the time until the stochastic process first enters $A$ .

1 Examples
2 Latent vs observable
3 See also
4 References

Examples

A common example of a first-hitting-time model is a ruin problem, such as Gambler's ruin. In this example, an entity (often described as a gambler or an insurance company) has an amount of money which varies randomly with time, possibly with some drift. The model considers the event that the amount of money reaches 0, representing bankruptcy. The model can answer questions such as the probability that this occurs within finite time, or the mean time until which it occurs.

First-hitting-time models can be applied to expected lifetimes, of patients or mechanical devices. When the process reaches an adverse threshold state for the first time, the patient dies, or the device breaks down.

Latent vs observable

In many real world applications, the process is latent, or unobservable. When first hitting time models are equipped with regression structures, accommodating covariate data, we call such regression structure Threshold regression. The threshold state, parameters of the process, and even time scale may depend on corresponding covariates.

A first-hitting-time (FHT) model has two underlying components: (1) a parent stochastic process 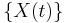$\{X(t)\}\,\,$ , and (2) a threshold. The first hitting time is defined as the time when the stochastic process first reaches the threshold. It is very important to distinguish whether the sample path of the parent process is latent (i.e., unobservable) or observable, and such distinction is a characteristic of the FHT model. By far, latent processes are most common. To give an example, we can use a Wiener process 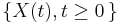$\{X(t), t\ge0\,\}\,$ as the parent stochastic process. 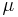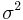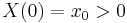Such Wiener process can be defined with the mean parameter ${\mu}\,\,$ , the variance parameter ${\sigma^2}\,\,$ , and the initial value $X(0)=x_0>0\,$ .

References

Whitmore, G. A. (1986). "First passage time models for duration data regression structures and competing risks", The Statistician, 35, 207–219. JSTOR 2987525
Whitmore, G. A. (1995). "Estimating degradation by a Wiener diffusion process subject to measurement error", Lifetime Data Analysis, 1, 307-319.
Whitmore, G. A., M. J. Crowder and J. F. Lawless (1998). "Failure inference from a marker process based on a bivariate Wiener model", Lifetime Data Analysis, 4, 229-251.
Redner, S (2001). A Guide to First-Passage Processes, Cambridge University Press. ISBN 0521652480

Statistics

Descriptive statistics

Continuous data

Location	Mean (Arithmetic, Geometric, Harmonic) Median Mode

Dispersion	Range Standard deviation Coefficient of variation Percentile Interquartile range

Shape	Variance Skewness Kurtosis Moments L-moments

Count data

Index of dispersion

Summary tables

Dependence

Statistical graphics

Data collection

Designing studies	Effect size Standard error Statistical power Sample size determination

Survey methodology	Sampling Stratified sampling Opinion poll Questionnaire

Controlled experiment	Design of experiments Randomized experiment Random assignment Replication Blocking Factorial experiment Optimal design

Uncontrolled studies	Natural experiment Quasi-experiment Observational study

Statistical inference

Statistical theory	Sampling distribution Sufficient statistic Meta-analysis

Bayesian inference	Bayesian probability Prior Posterior Credible interval Bayes factor Bayesian estimator Maximum posterior estimator

Frequentist inference	Confidence interval Hypothesis testing Likelihood-ratio

Specific tests	Z-test (normal) Student's t-test F-test Pearson's chi-squared test Wald test Mann–Whitney U Shapiro–Wilk Signed-rank Kolmogorov–Smirnov test

General estimation	Bias Robustness Efficiency Maximum likelihood Method of moments Minimum distance Density estimation

Correlation and regression analysis

Correlation	Pearson product-moment correlation Partial correlation Confounding variable Coefficient of determination

Regression analysis	Errors and residuals Regression model validation Mixed effects models Simultaneous equations models

Linear regression	Simple linear regression Ordinary least squares General linear model Bayesian regression

Non-standard predictors	Nonlinear regression Nonparametric Semiparametric Isotonic Robust

Generalized linear model	Exponential families Logistic (Bernoulli) Binomial Poisson

Partition of variance	Analysis of variance (ANOVA) Analysis of covariance Multivariate ANOVA Degrees of freedom

Categorical, multivariate, time-series, or survival analysis

Categorical data	Cohen's kappa Contingency table Graphical model Log-linear model McNemar's test

Multivariate statistics	Multivariate regression Principal components Factor analysis Cluster analysis Copulas

Time series analysis	Decomposition (Trend, Stationary process) ARMA model ARIMA model Vector autoregression Spectral density estimation

Survival analysis	Survival function Kaplan–Meier Logrank test Failure rate Proportional hazards models Accelerated failure time model

Applications

Biostatistics	Bioinformatics Biometrics Clinical trials & studies Epidemiology Medical statistics

Engineering statistics	Chemometrics Methods engineering Probabilistic design Process & Quality control Reliability System identification

Social statistics	Actuarial science Census Crime statistics Demography Econometrics National accounts Official statistics Population Psychometrics

Spatial statistics	Cartography Environmental statistics Geographic information system Geostatistics Kriging

Category
Portal
Outline
Index

First-hitting-time model

Contents

Examples

Latent vs observable

See also

References